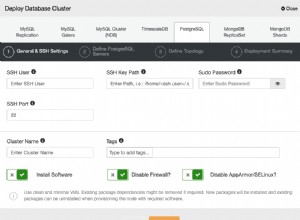
क्या डॉलर राशि के लिए फ्लोट या दशमलव डेटा प्रकार का उपयोग किया जाना चाहिए?
उत्तर आसान है। कभी नहीं तैरता। कभी नहीं !
फ्लोट्स आईईईई 754 के अनुसार हमेशा बाइनरी थे, केवल नए मानक आईईईई 754 आर परिभाषित दशमलव प्रारूप। कई भिन्नात्मक बाइनरी भाग कभी भी सटीक दशमलव प्रतिनिधित्व के बराबर नहीं हो सकते हैं।
किसी भी बाइनरी नंबर को m/2^n . के रूप में लिखा जा सकता है (m , n धनात्मक पूर्णांक), कोई भी दशमलव संख्या m/(2^n*5^n) . के रूप में .क्योंकि बायनेरिज़ में प्राइम factor 5 का अभाव है , सभी बाइनरी नंबरों को दशमलव द्वारा सटीक रूप से दर्शाया जा सकता है, लेकिन इसके विपरीत नहीं।
0.3 = 3/(2^1 * 5^1) = 0.3
0.3 = [0.25/0.5] [0.25/0.375] [0.25/3.125] [0.2825/3.125]
1/4 1/8 1/16 1/32
तो आप दी गई दशमलव संख्या से अधिक या कम संख्या के साथ समाप्त होते हैं। हमेशा।
यह तथ्य इतना मायने क्यों रखता हे? गोलाई।
सामान्य गोलाई का अर्थ है 0..4 नीचे, 5..9 ऊपर। तो यह करता है कोई फर्क नहीं पड़ता अगर परिणाम या तो 0.049999999999 . है .... या 0.0500000000 ... आप जानते होंगे कि इसका मतलब 5 सेंट होता है, लेकिन कंप्यूटर को यह नहीं पता होता है और 0.4999 को गोल कर देता है ... डाउन (गलत) और 0.5000 ... ऊपर (दाएं)।
यह देखते हुए कि फ़्लोटिंग पॉइंट कंप्यूटेशंस के परिणाम में हमेशा छोटी त्रुटि शर्तें होती हैं, निर्णय शुद्ध भाग्य है। यदि आप बाइनरी नंबरों के साथ दशमलव राउंड-टू-ईवन हैंडलिंग चाहते हैं तो यह निराशाजनक हो जाता है।
असंबद्ध? आप इस बात पर जोर देते हैं कि आपके अकाउंट सिस्टम में सब कुछ बिल्कुल ठीक है? एसेट्स और लायबिलिटी बराबर? ठीक है, फिर प्रत्येक प्रविष्टि के दिए गए स्वरूपित संख्याओं में से प्रत्येक को लें, उन्हें पार्स करें और उन्हें एक स्वतंत्र दशमलव प्रणाली के साथ जोड़ दें!
इसकी तुलना स्वरूपित योग से करें। उफ़, कुछ गड़बड़ है, है ना?
<ब्लॉकक्वॉट>उस गणना के लिए, अत्यधिक सटीकता और निष्ठा की आवश्यकता थी (हमने Oracle'sFLOAT का उपयोग किया) ताकि हम अर्जित होने वाले "बिलियनवाँ" को रिकॉर्ड कर सकें।
यह इस त्रुटि के खिलाफ मदद नहीं करता है। क्योंकि सभी लोग स्वचालित रूप से यह मान लेते हैं कि कंप्यूटर का योग सही है, और व्यावहारिक रूप से कोई भी स्वतंत्र रूप से जांच नहीं करता है।