वापसी संयोजन
संख्या तालिका या संख्या-जनरेटिंग सीटीई का उपयोग करके, 0 से 2^एन - 1 का चयन करें। संयोजन में रिश्तेदार सदस्यों की उपस्थिति या अनुपस्थिति को इंगित करने के लिए इन संख्याओं में 1s वाले बिट पदों का उपयोग करना, और उन लोगों को समाप्त करना जिनके पास नहीं है मानों की सही संख्या, आप अपने इच्छित सभी संयोजनों के साथ एक परिणाम सेट वापस करने में सक्षम होना चाहिए।
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
यह क्वेरी बहुत अच्छा प्रदर्शन करती है, लेकिन मैंने इसे अनुकूलित करने का एक तरीका सोचा, निफ्टी पैरेलल बिट काउंट पहले एक बार में ली गई वस्तुओं की सही संख्या प्राप्त करने के लिए। यह 3 से 3.5 गुना तेज (सीपीयू और समय दोनों) परफॉर्म करता है:
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
मैंने जाकर बिट-काउंटिंग पेज पढ़ा और सोचा कि यह बेहतर प्रदर्शन कर सकता है अगर मैं% 255 नहीं करता लेकिन बिट अंकगणित के साथ सभी तरह से जाता हूं। जब मुझे मौका मिलता है तो मैं इसे आजमाउंगा और देखूंगा कि यह कैसे ढेर हो जाता है।
मेरे प्रदर्शन के दावे ORDER BY खंड के बिना चलने वाले प्रश्नों पर आधारित हैं। स्पष्टता के लिए, यह कोड क्या कर रहा है Num . में सेट 1-बिट्स की संख्या गिन रहा है Numbers . से मेज़। ऐसा इसलिए है क्योंकि संख्या का उपयोग एक प्रकार के सूचकांक के रूप में किया जा रहा है, यह चुनने के लिए कि सेट के कौन से तत्व वर्तमान संयोजन में हैं, इसलिए 1-बिट्स की संख्या समान होगी।
मुझे आशा है कि आपको यह पसंद आएगा!
रिकॉर्ड के लिए, एक सेट के सदस्यों का चयन करने के लिए पूर्णांकों के बिट पैटर्न का उपयोग करने की यह तकनीक है जिसे मैंने "वर्टिकल क्रॉस जॉइन" बनाया है। यह प्रभावी रूप से डेटा के कई सेटों के क्रॉस जॉइन में परिणत होता है, जहां सेट और क्रॉस जॉइन की संख्या मनमानी होती है। यहां, सेट की संख्या एक बार में लिए गए आइटम की संख्या है।
वास्तव में सामान्य क्षैतिज अर्थ में क्रॉस जॉइनिंग (प्रत्येक जॉइन के साथ कॉलम की मौजूदा सूची में अधिक कॉलम जोड़ने का) कुछ इस तरह दिखेगा:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
उपरोक्त मेरे प्रश्न प्रभावी रूप से "क्रॉस जॉइन" के रूप में कई बार केवल एक शामिल होने के साथ आवश्यक हैं। वास्तविक क्रॉस जॉइन की तुलना में परिणाम अप्रकाशित हैं, निश्चित रूप से, लेकिन यह एक छोटी सी बात है।
आपके कोड की आलोचना
सबसे पहले, क्या मैं आपके फैक्टोरियल यूडीएफ में इस बदलाव का सुझाव दे सकता हूं:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
अब आप संयोजनों के बहुत बड़े सेटों की गणना कर सकते हैं, साथ ही यह अधिक कुशल है। आप decimal(38, 0) . का उपयोग करने पर भी विचार कर सकते हैं अपने संयोजन गणनाओं में बड़ी मध्यवर्ती गणनाओं की अनुमति देने के लिए।
दूसरा, आपकी दी गई क्वेरी सही परिणाम नहीं लौटाती है। उदाहरण के लिए, नीचे दिए गए प्रदर्शन परीक्षण से मेरे परीक्षण डेटा का उपयोग करते हुए, सेट 1 सेट 18 के समान है। ऐसा लगता है कि आपकी क्वेरी एक स्लाइडिंग पट्टी लेती है जो चारों ओर लपेटती है:प्रत्येक सेट हमेशा 5 आसन्न सदस्य होते हैं, कुछ इस तरह दिखते हैं (मैंने पिवोट किया इसे देखना आसान बनाने के लिए):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
मेरे प्रश्नों के पैटर्न की तुलना करें:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
बस बिट-पैटर्न ड्राइव करने के लिए -> संयोजन चीज़ के सूचकांक को किसी के लिए घर पर, ध्यान दें कि बाइनरी में 31 =11111 और पैटर्न एबीसीडीई है। 121 बाइनरी में 1111001 है और पैटर्न A__DEFG (बैकवर्ड मैप) है।
वास्तविक संख्या तालिका के साथ प्रदर्शन परिणाम
मैंने ऊपर अपनी दूसरी क्वेरी पर बड़े सेट के साथ कुछ प्रदर्शन परीक्षण चलाया। मेरे पास इस समय उपयोग किए गए सर्वर संस्करण का कोई रिकॉर्ड नहीं है। यह रहा मेरा परीक्षण डेटा:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
पीटर ने दिखाया कि यह "वर्टिकल क्रॉस जॉइन" प्रदर्शन नहीं करता है और साथ ही गतिशील एसक्यूएल लिखने के लिए वास्तव में क्रॉस जॉइन से बचाता है। कुछ और पढ़ने की मामूली कीमत पर, उनके समाधान में मेट्रिक्स 10 से 17 गुना बेहतर है। काम की मात्रा बढ़ने के साथ-साथ उसकी क्वेरी का प्रदर्शन मेरी तुलना में तेज़ी से घटता है, लेकिन इतनी तेज़ नहीं कि किसी को भी इसका इस्तेमाल करने से रोक सके।
नीचे दी गई संख्याओं का दूसरा सेट वह कारक है जिसे तालिका में पहली पंक्ति से विभाजित किया जाता है, बस यह दिखाने के लिए कि यह कैसे मापता है।
एरिक
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
पीटर
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
एक्सट्रपलेशन, अंततः मेरी क्वेरी सस्ती होगी (हालाँकि यह शुरुआत से ही पढ़ी जाती है), लेकिन लंबे समय तक नहीं। सेट में 21 आइटम का उपयोग करने के लिए पहले से ही 2097152 तक की संख्या तालिका की आवश्यकता है...
यहां एक टिप्पणी है जिसे मैंने मूल रूप से यह महसूस करने से पहले किया था कि मेरा समाधान ऑन-द-फ्लाई नंबर तालिका के साथ काफी बेहतर प्रदर्शन करेगा:
ऑन-द-फ्लाई नंबर तालिका के साथ प्रदर्शन परिणाम
जब मैंने मूल रूप से यह उत्तर लिखा, तो मैंने कहा:
खैर, मैंने इसे आजमाया, और परिणाम यह हुआ कि इसने बहुत बेहतर प्रदर्शन किया! यहाँ वह क्वेरी है जिसका मैंने उपयोग किया है:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
ध्यान दें कि मैंने सब कुछ परीक्षण करने के लिए आवश्यक समय और स्मृति को कम करने के लिए मानों को चर में चुना है। सर्वर अभी भी वही काम करता है। मैंने पीटर के संस्करण को समान होने के लिए संशोधित किया, और अनावश्यक अतिरिक्त हटा दिए ताकि वे दोनों जितना संभव हो उतना दुबला हो। इन परीक्षणों के लिए उपयोग किया जाने वाला सर्वर संस्करण है Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) VM पर चल रहा है।
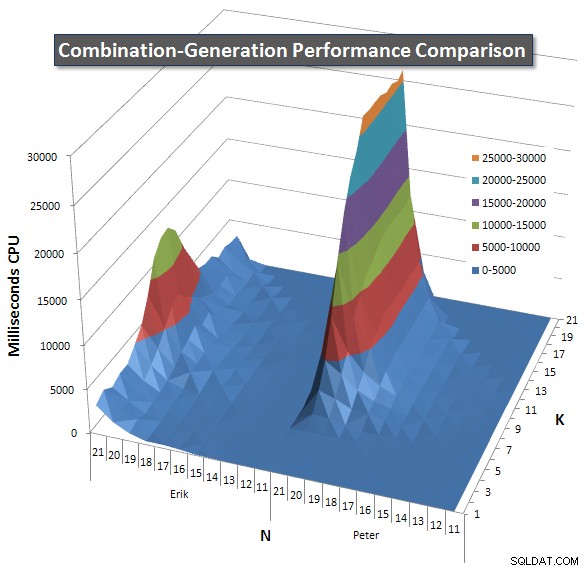
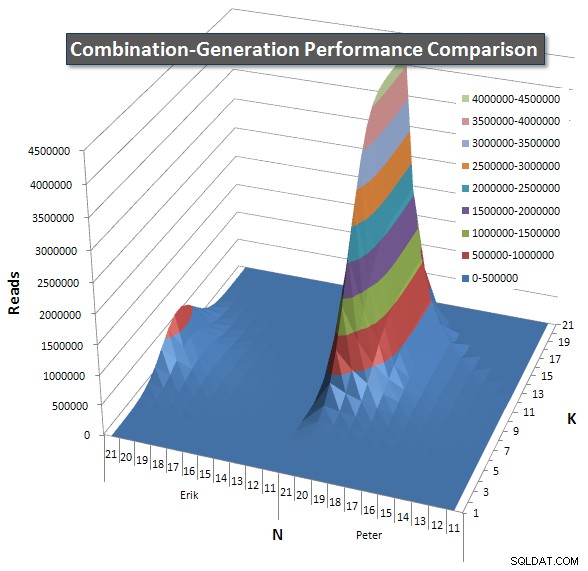
नीचे 21 तक N और K के मानों के लिए प्रदर्शन वक्र दिखाने वाले चार्ट हैं। उनके लिए आधार डेटा इस पृष्ठ पर एक और उत्तर . मान प्रत्येक K और N मान पर प्रत्येक क्वेरी के 5 रन का परिणाम होते हैं, इसके बाद प्रत्येक मीट्रिक के लिए सर्वोत्तम और सबसे खराब मानों को निकाल दिया जाता है और शेष 3 का औसत निकाला जाता है।
मूल रूप से, मेरे संस्करण में N के उच्च मूल्यों और K के निम्न मानों पर "कंधे" (चार्ट के सबसे बाएं कोने में) है जो इसे गतिशील SQL संस्करण की तुलना में खराब प्रदर्शन करता है। हालांकि, यह काफी कम और स्थिर रहता है, और एन =21 और के =11 के आसपास का केंद्रीय शिखर डायनेमिक एसक्यूएल संस्करण की तुलना में अवधि, सीपीयू और रीड के लिए बहुत कम है।
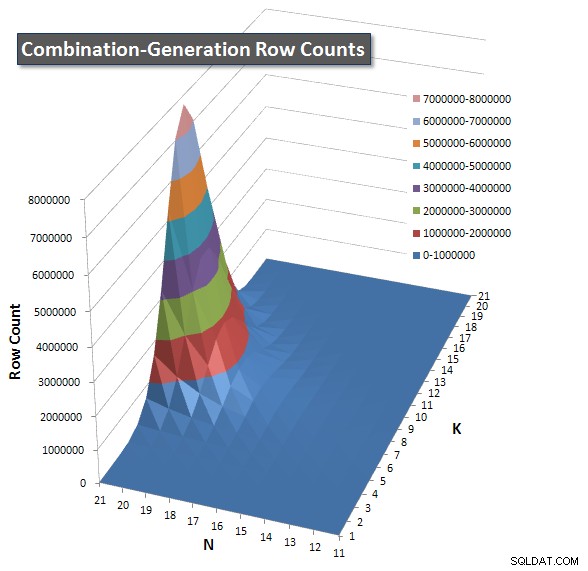
मैंने पंक्तियों की संख्या का एक चार्ट शामिल किया है जिसमें प्रत्येक आइटम के वापस आने की उम्मीद है ताकि आप देख सकें कि क्वेरी को कितना बड़ा काम करना है, इसके मुकाबले कैसे प्रदर्शन किया जाता है।
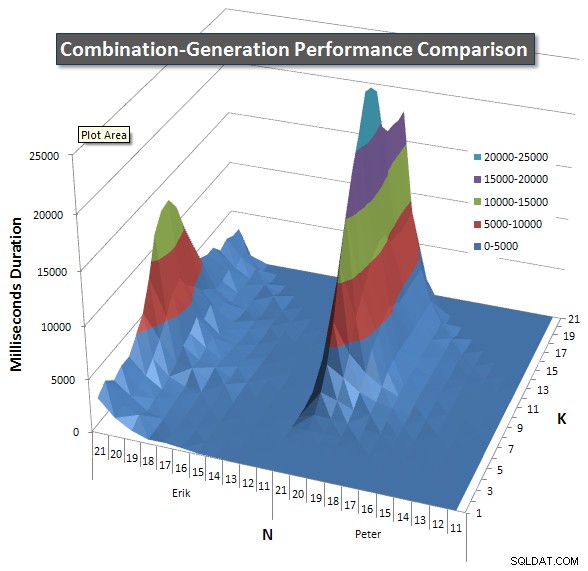
कृपया देखें इस पेज पर मेरा अतिरिक्त जवाब पूर्ण प्रदर्शन परिणामों के लिए। मैंने पोस्ट कैरेक्टर लिमिट को हिट किया और इसे यहां शामिल नहीं कर सका। (कोई भी विचार इसे और कहां रखा जाए?) मेरे पहले संस्करण के प्रदर्शन परिणामों के परिप्रेक्ष्य में चीजों को रखने के लिए, यहां पहले जैसा ही प्रारूप है:
एरिक
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
पीटर
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
निष्कर्ष
- पंक्तियों वाली वास्तविक तालिका की तुलना में ऑन-द-फ्लाई नंबर टेबल बेहतर होते हैं, क्योंकि बड़ी पंक्तियों में एक को पढ़ने के लिए बहुत सारे I/O की आवश्यकता होती है। थोड़ा सीपीयू का उपयोग करना बेहतर है।
- मेरे प्रारंभिक परीक्षण वास्तव में दो संस्करणों की प्रदर्शन विशेषताओं को दिखाने के लिए पर्याप्त व्यापक नहीं थे।
- पीटर के संस्करण में सुधार किया जा सकता है, प्रत्येक जॉइन को न केवल पिछले आइटम से बड़ा बनाया जा सकता है, बल्कि सेट में कितनी अधिक वस्तुओं को फिट करने के आधार पर अधिकतम मूल्य को प्रतिबंधित किया जा सकता है। उदाहरण के लिए, एक बार में 21 लिए गए 21 आइटम पर, 21 पंक्तियों (सभी 21 आइटम, एक बार) का केवल एक उत्तर होता है, लेकिन गतिशील SQL संस्करण में मध्यवर्ती पंक्तियों में, निष्पादन योजना की शुरुआत में, जैसे संयोजन होते हैं " AU" चरण 2 पर है, भले ही इसे अगले जॉइन पर छोड़ दिया जाएगा क्योंकि "U" से अधिक कोई मूल्य उपलब्ध नहीं है। इसी तरह, चरण 5 पर एक मध्यवर्ती रोसेट में "ARSTU" होगा लेकिन इस बिंदु पर एकमात्र मान्य कॉम्बो "ABCDE" है। इस उन्नत संस्करण में केंद्र में एक निचला शिखर नहीं होगा, इसलिए संभवत:स्पष्ट विजेता बनने के लिए इसे पर्याप्त रूप से सुधारना नहीं है, लेकिन यह कम से कम सममित हो जाएगा ताकि चार्ट क्षेत्र के मध्य में अधिकतम नहीं रहेंगे बल्कि वापस गिर जाएंगे मेरे संस्करण के अनुसार 0 के करीब (प्रत्येक क्वेरी के लिए चोटियों के शीर्ष कोने को देखें)।
अवधि विश्लेषण
- अवधि (>100ms) में संस्करणों के बीच वास्तव में कोई महत्वपूर्ण अंतर नहीं है जब तक कि 14 आइटम एक बार में 12 नहीं लिए जाते। इस बिंदु तक, मेरा संस्करण 30 बार जीतता है और गतिशील SQL संस्करण 43 बार जीतता है।
- 14•12 से शुरू होकर, मेरा संस्करण 65 गुना (59>100ms), गतिशील SQL संस्करण 64 गुना (60>100ms) तेज था। हालाँकि, हर समय मेरा संस्करण तेज़ था, इसने कुल औसत अवधि 256.5 सेकंड बचाई, और जब गतिशील SQL संस्करण तेज़ था, तो इसने 80.2 सेकंड की बचत की।
- सभी परीक्षणों की कुल औसत अवधि एरिक 270.3 सेकंड, पीटर 446.2 सेकंड थी।
- यदि यह निर्धारित करने के लिए एक लुकअप तालिका बनाई गई थी कि किस संस्करण का उपयोग करना है (इनपुट के लिए तेज़ को चुनना), तो सभी परिणाम 188.7 सेकंड में किए जा सकते हैं। हर बार सबसे धीमी गति का उपयोग करने में 527.7 सेकंड लगेंगे।
विश्लेषण पढ़ता है
अवधि विश्लेषण ने मेरी क्वेरी को महत्वपूर्ण रूप से जीतते हुए दिखाया, लेकिन अधिक मात्रा में नहीं। जब मीट्रिक को रीड पर स्विच किया जाता है, तो एक बहुत ही अलग तस्वीर उभरती है--मेरी क्वेरी औसतन 1/10वां रीड का उपयोग करती है।
- पढ़े गए संस्करणों (>1000) के बीच वास्तव में कोई महत्वपूर्ण अंतर नहीं है जब तक कि एक बार में 9 आइटम नहीं ले लिए जाते। इस बिंदु तक, मेरा संस्करण 30 बार जीतता है और गतिशील SQL संस्करण 17 बार जीतता है।
- 9•9 से शुरू होकर, मेरे संस्करण ने 118 बार (113>1000), गतिशील SQL संस्करण 69 बार (31>1000) कम पढ़े। हालांकि, हर बार मेरे संस्करण ने कम रीड्स का उपयोग किया, इसने कुल औसत 75.9M रीड्स को बचाया, और जब डायनेमिक SQL संस्करण तेज था, तो इसने 380K रीड्स को बचाया।
- सभी परीक्षणों के लिए कुल औसत पढ़ा गया एरिक 8.4M, पीटर 84M था।
- यदि यह निर्धारित करने के लिए एक लुकअप तालिका बनाई गई थी कि किस संस्करण का उपयोग करना है (इनपुट के लिए सबसे अच्छा चुनना), तो सभी परिणाम 8M रीड्स में किए जा सकते हैं। हर बार सबसे खराब का उपयोग करने में 84.3M रीड्स लगेंगे।
मुझे एक अद्यतन गतिशील SQL संस्करण के परिणाम देखने में बहुत दिलचस्पी होगी जो प्रत्येक चरण में चुने गए आइटम पर अतिरिक्त ऊपरी सीमा रखता है जैसा कि मैंने ऊपर वर्णित किया है।
परिशिष्ट
मेरी क्वेरी का निम्न संस्करण ऊपर सूचीबद्ध प्रदर्शन परिणामों की तुलना में लगभग 2.25% का सुधार प्राप्त करता है। मैंने MIT की HAKMEM बिट-काउंटिंग पद्धति का उपयोग किया, और एक Convert(int) जोड़ा। row_number() . के परिणाम पर चूंकि यह एक बड़ा रिटर्न देता है। निश्चित रूप से मैं चाहता हूं कि यह वह संस्करण है जिसका उपयोग मैंने ऊपर के सभी प्रदर्शन परीक्षण और चार्ट और डेटा के लिए किया था, लेकिन इसकी संभावना नहीं है कि मैं इसे कभी भी फिर से करूंगा क्योंकि यह श्रम-गहन था।
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
और मैं एक और संस्करण दिखाने का विरोध नहीं कर सका जो बिट्स की गिनती प्राप्त करने के लिए लुकअप करता है। यह अन्य संस्करणों की तुलना में तेज़ भी हो सकता है:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))