यदि आप एक सन्निकटन एल्गोरिथ्म की तलाश कर रहे हैं, तो मैं एक k- साधन एल्गोरिथ्म या एक पदानुक्रमित क्लस्टर, विशेष रूप से एक राक्षस वक्र या एक अंतरिक्ष भरने वाले वक्र की तलाश करने का सुझाव देता हूं। सबसे पहले आप ग्राफ के न्यूनतम फैले हुए पेड़ की गणना कर सकते हैं और फिर सबसे लंबे और महंगे किनारों को हटा सकते हैं। फिर पेड़ कई छोटे पेड़ बनाता है और आप k- साधन का उपयोग बिंदुओं के समूह यानी क्लस्टर की गणना करने के लिए कर सकते हैं।
"एकल-लिंक के-क्लस्टरिंग एल्गोरिदम ... ठीक क्रुस्कल का एल्गोरिदम है ... एमएसटी खोजने और के-1 सबसे महंगे किनारों को हटाने के बराबर।" उदाहरण के लिए यहां देखें:https://stats.stackexchange.com/ प्रश्न/1475/विज़ुअलाइज़ेशन-सॉफ़्टवेयर-फॉर-क्लस्टरिंग .
राक्षस वक्र के लिए एक अच्छा उदाहरण हिल्बर्ट वक्र है। इस वक्र का मूल रूप एक यू-आकार है और इसमें से कई को एक साथ कॉपी करके और इसे घुमाकर वक्र यूक्लिडियन स्थान को भर देता है। आश्चर्यजनक रूप से एक ग्रे कोड इस यू-आकार के उन्मुखीकरण का पता लगाने में मदद कर सकता है। आप निक के स्थानिक सूचकांक क्वाडट्री हिल्बर्ट वक्र को देख सकते हैं अधिक विवरण के बारे में ब्लॉग लेख . वक्र के सूचकांक की गणना करने के बजाय आप बिंग मैप्स की तरह एक क्वाडकी को एक साथ रख सकते हैं। क्वाडकी प्रत्येक समन्वय के लिए अद्वितीय है और इसका उपयोग सामान्य स्ट्रिंग संचालन के साथ किया जा सकता है। कुंजी में प्रत्येक स्थिति यू-आकार वक्र का हिस्सा है और इस प्रकार आप क्वाडकी से आंशिक रूप से बाएं से दाएं चयन से बिंदुओं के इस क्षेत्र का चयन कर सकते हैं।
इस छवि में आप देख सकते हैं कि हरे रंग का बहुभुज हिल्बर्ट वक्र का उपयोग करते हुए पाया जाता है:
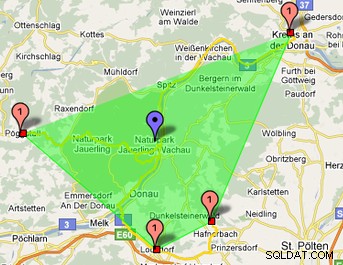
आप मेरी php कक्षाएं यहां पा सकते हैं:https://www.phpclasses.org/package/6202-PHP-Generate-points-of-an-Hilbert-curve.html